Тригонометричні формули — це одна з основних тем в математиці, зокрема в геометрії та алгебрі. Вони використовуються для розв’язування задач з трикутниками, колами, гармонічними коливаннями й навіть у фізиці. У цій статті ми розглянемо всі основні тригонометричні формули, пояснимо їх значення і навчимося застосовувати їх на практиці.
Що таке тригонометричні формули
Тригонометричні формули — це математичні вирази, що описують співвідношення між сторонами та кутами в трикутниках. Зокрема, вони пов’язують тригонометричні функції, такі як синус, косинус, тангенс і котангенс.
Основні тригонометричні функції
Перед тим як перейти до формул, розглянемо основні функції:
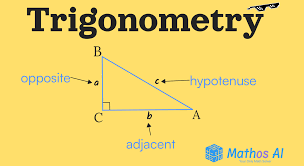
- Синус (sin) — це відношення протилежного катета до гіпотенузи.
- Косинус (cos) — це відношення прилеглого катета до гіпотенузи.
- Тангенс (tan) — це відношення синуса до косинуса.
- Котангенс (cot) — це обернене до тангенса.
Ці функції — основа для розуміння всіх подальших формул.
Тригонометричні формули в прямокутному трикутнику
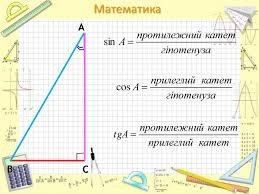
У прямокутному трикутнику тригонометричні функції виглядають наступним чином:
- sin(α) = протилежний катет / гіпотенуза
- cos(α) = прилеглий катет / гіпотенуза
- tan(α) = протилежний катет / прилеглий катет
- cot(α) = прилеглий катет / протилежний катет
Ці формули є основою для розрахунків у геометрії.
Основні тригонометричні тотожності
Ще один важливий набір формул — це тригонометричні тотожності. Вони включають:
- sin²x + cos²x = 1
- 1 + tan²x = 1/cos²x
- 1 + cot²x = 1/sin²x
Ці рівняння допомагають спрощувати вирази та розв’язувати рівняння.
Формули подвійного кута
Формули для подвоєння кута дозволяють обчислити значення функцій від подвоєного кута:
- sin(2x) = 2sin(x)cos(x)
- cos(2x) = cos²(x) – sin²(x)
- tan(2x) = 2tan(x) / (1 – tan²(x))
Ці формули корисні в аналітичній геометрії та фізиці.
Формули половинного кута
Якщо потрібно розрахувати значення функцій від половини кута, використовують такі формули:
- sin(x/2) = ±√((1 – cos(x)) / 2)
- cos(x/2) = ±√((1 + cos(x)) / 2)
- tan(x/2) = ±√((1 – cos(x)) / (1 + cos(x)))
Знак залежить від чверті кола, в якій знаходиться кут.
Формули суми і різниці кутів
Ці формули дозволяють обчислювати значення функцій від суми чи різниці двох кутів:
- sin(a ± b) = sin(a)cos(b) ± cos(a)sin(b)
- cos(a ± b) = cos(a)cos(b) ∓ sin(a)sin(b)
- tan(a ± b) = (tan(a) ± tan(b)) / (1 ∓ tan(a)tan(b))
Вони особливо важливі при розв’язанні складних виразів.
Обернені тригонометричні функції
Не менш важливими є й обернені функції:
- arcsin(x)
- arccos(x)
- arctan(x)
- arccot(x)
Ці функції допомагають знаходити значення кутів за відомими значеннями функцій.
Тригонометричні формулии в радіанах
При роботі з колом або гармонічними коливаннями кути часто вимірюють у радіанах. Один радіан — це кут, при якому довжина дуги дорівнює радіусу. Формули залишаються тими ж, але кут потрібно задавати в радіанах.
Практичне застосування тригонометричних формул
Тригонометричні формулии використовуються не лише в математиці. Їх застосовують у:
- Фізиці (розрахунок коливань, хвиль, сили);
- Інженерії (моделювання руху, механіка);
- Астрономії (обчислення координат зірок);
- Будівництві (визначення кутів нахилу дахів, сходів).
Таким чином, знання формул відкриває шлях до точних розрахунків у багатьох сферах.
Поради щодо вивчення тригонометрії
Навчитися використовувати тригонометричні формули легко, якщо слідувати кільком порадам:
- Починайте з базових понять: синус і косинус.
- Пам’ятайте тотожності, вони часто зберігаються в пам’яті автоматично.
- Практикуйтесь на задачах: чим більше прикладів — тим краще засвоєння.
- Візуалізуйте кути на одиничному колі — це допомагає зрозуміти знак функції.
Поширені помилки при використанні тригонометричних формул
Хоча формули виглядають просто, помилки трапляються досить часто:
- Забування про знак кута (особливо в ІІІ та ІV чвертях).
- Неправильне перетворення формул (наприклад, неправильно використана тотожність).
- Використання градусів замість радіанів або навпаки.
Тому важливо завжди перевіряти свої дії та формулювання.
Читати далі: Що таке «дорівнює» – просте пояснення для школярів
FAQ: Часті запитання про тригонометричні формули
Тригонометричні формули — це математичні рівняння, які описують зв’язок між сторонами і кутами в трикутнику за допомогою тригонометричних функцій.
Найкраще — через практику. Виконуйте багато вправ, вивчайте тотожності, застосовуйте у задачах.
У фізиці, архітектурі, будівництві, навігації, астрономії та інженерії — скрізь, де важлива точність розрахунків.
На іспитах тригонометрія часто зустрічається в задачах з графіками, рівняннями та площинами. Її добре знати — це ваш плюс до балів.
Висновок
Тригонометричні формули — це важлива складова математичної освіти. Вони дозволяють розв’язувати складні задачі просто та ефективно. Якщо ви бажаєте краще зрозуміти геометрію, фізику або інженерію — почніть із вивчення цих формул. З часом це стане вашим потужним інструментом у навчанні й житті.

